Introduction to GNSS Tracking and Kalman Filtering
Modern mass-market GNSS software receivers rely on tracking architectures developed from analogue signal processing techniques developed in the early 20th century. Although these methods have proven themselves to be reliable and sufficient for most GNSS applications, newer applications which aim to push the boundaries of what can be done with GNSS could benefit from more versatile, modern, tracking techniques. The basis of many of these cutting edge techniques is the Kalman filter: an iterative signal processing technique which aims to estimate the internal parameters of a system based on noisy observations of its external measurements.
Within the context of GNSS, Kalman filtering has been shown experimentally to be a powerful tool for performing carrier synchronization, an important step in the GNSS datapath in which the receiver identifies the timing properties of the received signal (i.e. carrier phase and Doppler shift) so that the signal can be decoded to determine the transmitted message. In fact, the principle of carrier synchronization is present with any digital communication, but in the case of GNSS, carrier synchronization preforms two roles: not only are the timing parameters needed in order to decode the navigation data transmitted by the satellite, carrier phase and Doppler shift are also two of the observables required to get a position fix.

"Comparison of PLL-DLL tracking to tracking to Extended Kalman filter tracking of GPS L1 C/A signal recorded at CTTC in 2013 under nearly ideal conditions. Note the highly improved signal-to-noise ratio in the Carrier Frequency and Code Frequency observables."
Kalman filtering and more advanced techniques derived from the Kalman filter, may provide immediate benefits to performance under adverse conditions. Moreover, a transition from traditional architectures to Kalman architectures will open the gateway to potential reimaginings of the GNSS signal processing pathway which may allow GNSS receivers to operate under extremely harsh conditions, and may greatly expand upon the places in which GNSS technology may be used.
Challenges involved in Kalman Filtering
Although Kalman filtering may be a powerful tool with the right planning, it is a technique which involves working through several caveats and critical challenges in order to be properly integrated into a given application. One of the most important of these practical challenges is the assumption of a well defined model of the process and measurement noise covariances, but this information is not directly available a priori and may change as channel conditions change during system operation. Traditionally, these values are estimated a priori through time series analysis, and are implemented within the Kalman filter as constant values Q and R. In general, however, there is no requirement within the Kalman filter that they must be constant, and may instead take time-varying values Qt-1 and Rt. Several methods have been proposed to estimate and update these noise characteristics iteratively as the filter operates. These methods, however, rely on frequentist methods which do not guarantee validity of the noise covariance matrix.
One of the key goals of our 2018 Google Summer of Code contribution to the GNSS-SDR open-source project project was to develop a Bayesian estimation architecture for estimating the covariance of the measurement noise during filter operation. For more information about that contribition, please see our report on the matter here. The formulation for that embedded Bayesian filter relies on the innovations process of the estimation being a zero-mean white noise sequence. Conveniently, this sequence has been shown to be white in the Kalman filter literature, but only under conditions of \emph{optimal} filter performance (i.e. with precise predictions based on an accurate model). Our initial 2018 effort to incorporate this methodology into GNSS-SDR involved the use of extended Kalman filter (EKF) architectures for performing nonlinear state estimation and tracking. Ultimately, the performance of the Bayesian covariance estimation (BCE) filter under this approach did not meet the standard required for maintaining carrier synchronization over more than a few seconds. In our report for last year's Google Summer of Code we hypothesized that this issue might be mitigated by the use of a more precise nonlinear tracking procedure. As a follow-up to last year's contribution, this year we once again proposed a collaboration with the GNSS-SDR project with the following goals in mind:
- Development of modular libraries for easily implementing and utilizing various Kalman filter based nonlinear tracking algorithms, such as the Cubature Kalman filter and Unscented Kalman filter
- Incorporation of those libraries into a tracking block for performing discriminator free, Kalman filter based carrier phase, Doppler and Doppler rate estimation in the Tracking block of the GNSS-SDR receiver
- Incorporation of those libraries into a tracking block for performing discriminator free, Kalman filter based joint code-carrier tracking, including carrier phase, Doppler, Doppler rate
and code error
The tracking blocks and libraries which we will be referencing to throughout this document, and which will be the subject of most of the changes referenced as part of this Google Summer of Code contirbution may be found within our fork of the GNSS-SDR repository here.
Project development
The following sections contain a brief discription of the work done for each of these contributions. A PDF document containing a more comprehensive description of the
Nonlinear Tracking Libraries
One of the advantages in using a system architecture based on the Kalman filter is that it is relatively trivial to update the architecture to reflect changes in the signal model. In particular, Kalman filter architectures such as the cubature Kalman filter (CKF) and unscented Kalman filter (UKF) need only to be able to evaluate equations modelling the state time evolution and state-measurement relationship (hereafter transition and measurement equations). In contrast to the extended Kalman filter (EKF), no additional functions (e.g. Jacobian function) need to be provided. With this in mind, we developed generalized libraries for modular incorporation of nonlinear, Bayesian tracking algorithms into the GNSS-SDR tracking framework. These libraries can be found in the GNSS-SDR source directory as tracking_Gaussian_filter, tracking_models, and nonlinear_tracking.
The design philosophy of these classes is fairly straightforward: the TrackingGaussianFilter class provides a generic interface for storing the basic parameters of a second order state estimation filter: the state, state covariance, and additive noise covariances. The TrackingNonlinearFilter class inherits these parameters from TrackingGaussianFilter and adds generic functional templates representing the transition and measurement equations. These functionals are intended to be classes which inherit from the ModelFunction class laid out in the tracking_models.h library, and the functions that they specify are used to compute the model predicted state and mesurements within the Gaussian filter.
Using the TrackingNonlinearFunction Class
Use of the TrackingNonlinearFilter class is straightforward, but makes use of templates for modularity. Declaration of an instance of TrackingNonlinearFilter requires specifying three parameters: the class specified by NonlinearFilter indicates the type of Gaussian filter to use (e.g. UKF, CKF) as implemented in nonlinear_tracking.h, while OutputType1 and OutputType2 specify the output type of the state and measurement equations. These types are expected to be one of the data types from the Armadillo C++ library for linear algebra and scientific computing: in general either arma::colvec or arma::cx_vec. Once these parameters are specified, the object is instantiated and the filter may be initialized using set_params, however it is necessary to attach the model functions before the filter may be invoked with get_carrier_nco.
Using ModelFunction Functionals
One functional for each model function (i.e. transition and measurement) should defined adjacent to where they are to be used (e.g. in a particular GNU Radio block), and they must each inherit from the ModelFunction class. Additionally, each functional must override the () operator with a function that accepts a single arma::colvec as an input. The output type is specified by the template class parameter OutputType and

Once defined, an instance of the functional must be created and attached to an instance of TrackingNonlinearFilter using TrackingNonlinearFilter::set_model.
Using the GaussianFilter Class to create Filters
The class specifier NonlinearFilter in the template class TrackingNonlinearFilter specifies the type of nonlinear filter that should be used. In general, this should refer to a class which inherits from the GaussianFilter class specified in the nonlinear_tracking library. The GaussianFilter class represents the basic implementation of a second order Gaussian filter, and includes setters and getters for the mean and covariance of the state prediction and updated state estimation. The classes which inherit from it must specify the prediction and update steps of the Gaussian filter procedure as predict_sequential and update_sequential respectively. In our 2019 Google Summer of Code contribution we have developed and implemented two nonlinear filters: the unscented Kalman filter and the cubature Kalman filter. Unit tests for each of these implementaitons can be found in the GNSS-SDR source here. These blocks test the reliability and accuracy of the tracking algorithms by implementing a linear system with random parameters and comparing the output of the nonlinear filters to that of a standard linear Kalman filtering procedure. This test is repeated many times with random initialization and the test is declared as passed if and only the results of the nonlinear filter are within a certain acceptable range of the linear result for each one.
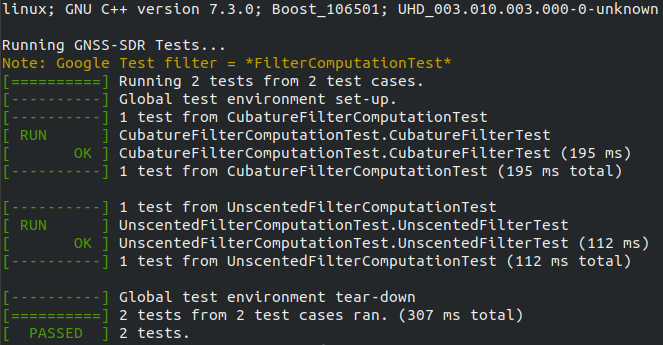
In future updates, other Kalman filter based nonlinear tracking implementations can be included in nonlinear_tracking.h based on these examples.
Mixed DLL+PLL Code and Kalman Carrier Tracking
Another goal of out 2019 Google Summer of Code contribution to the GNSS-SDR project was to develop a Kalman filter based, discriminator free carrier phase tracking implementation. Such an implementation uses a nonlinear Kalman filter to replace the FLL+PLL portion of the traditional locked loop architecture with a nonlinear Kalman filter for estimating the carrier phase, Doppler and Doppler rate parameters, while leaving estimation of the code error to the standard DLL. In order to be avoid the use of discriminator functions, the filter needs to operate based on a model which directly relates the carrier phase to the output of the correlation step. We attempted to create such an implementation in our 2018 Google Summer of Code contribution but encountered issues getting the method to work with signals which rely on tracking a pilot such as, for example, the those on the Galileo E1 band. To overcome this limitation, we designed a mixed tracking implementation based on the dll_pll_veml_tracking GNU radio tracking block which relies on the standard locked loop architecture and a two-quadrant arctangent discriminator for acquiring the pilot signal before handing off to a Gaussian filter architecture for performing real time carrier estimation. The code implementing this mixed tracking block can be found in the GNSS-SDR source repository as mixed_veml_tracking.
Discriminator free Carrier Tracking Model
As described in the literature, the correlator outputs are related to the carrier parameters by way of a complex exponential. For signals which make use of a pilot signals, such as Galileo E1, this subject to a sign change (+/-) depending on the bits of the pilot signal. Since the Kalman filter is not well suited to handling rapid changes, such as those associated with bit flips, it is necessary to remove the effect of the pilot bit. This is done by taking the measurement to be square of the correlator outputs. Separating the real and imaginary parts yields the following measurement model:

The state, is designed to incorporate the carrier parameters, namely carrier phase error, Doppler and Doppler rate, as well as the signal amplitude. The carrier parameters are modelled as evolving according to a quadratic transition model, also described in the literature, while the correlator output amplitude is assumed as being constant over time. The transition and measurement functions which comprise this model are implemented in mixed_veml_tracking.h. For a more thourough explanation of this tracking model, see the full PDF version of this report here.
Notes on Code Implementation
This code is adapted from

Testing and Results
Testing of the mixed_veml_tracking GNU radio block was performed by implementing an adapter block and unit test for running this tracking block with Galileo E1 signals. The tracking block and unit test can be found in the GNSS-SDR source repository here and here respectively. The adapter and unit test are based on those implemented for Galileo E1 DLL+PLL tracking and the unit test performs a large number of tracking iterations using a simulated Galileo E1B PRN E11 signal.

The mixed tracking implementation passed the unit test, and performed the same number of iterations as the DLL+PLL implementation in a slightly shorter amount of time.
Finally, the performance of the mixed tracking implementation was evaluated with real signals collected using a hardware receiver at CTTC in 2013. The recorded data was played back through the GNSS-SDR datapath using the Galileo E1 adapter for the mixed_veml_tracking GNU radio block and the output of the tracking dataloggers stored and plotted using MATLAB for visual analysis.
The above figure shows the results of the tracking for Galileo E1 PRN 11. It is evident from these results that the mixed tracking block is not able to track the carrier synchronization parameters with sufficient accuracy to acquire a position fix. Although this is not the result we were hoping for, the filter code was able to perform its task without error. With more time spent tuning the Kalman filter and model parameters, we're confident that the results of our mixed tracking block should match those of its DLL+PLL based counterpart.
Kalman Filter based Joint Code-Carrier Tracking
The final goal of out 2019 Google Summer of Code contribution to the GNSS-SDR project was to develop a Kalman filter based, discriminator free
Correlator output Joint Code-Carrier Model
The joint measurement model extends the model for the output of the correlation step as described previously to include the early and late outputs, as well as the relationship between the complex correlator outputs and the code error. A similar trick is used to get rid of the bit transitions as in the carrier tracking model as well, giving the updated measurement model

Separating the real and imaginary components of this and accounting for additive noise gives the final real valued measurement model to be used in the filter

The state is designed to incorporate the carrier parameters, code parameters, and the signal amplitude. The carrier parameters and signal amplitude are modelled as in the carrier tracking model, while the code error is modelled as

This transition function is parameterized by the sampling period and the number of code chips per radian, computed by multiplying the carrier frequency with the code period in chips. The functionals which implement the transition and measurement functions which comprise this model are located in joint_veml_tracking.h. As before, a more thourough explanation of this tracking model is provided in full PDF version of this report here.
Notes on Code Implementation
An important feature of this measurement model implementation is that, as previously described, the measurement model needs to be able to perform arbitrary evaluations of the autocorrelation function of the local code. To this end, the functional which implements this needs to be extended to include an instance of Cpu_Autocorrelator_Real_Codes, which may be found in the cpu_autocorrelator_real_codes library located here. This object adapts the Cpu_Multicorrelator_Real_Codes object: instead of accepting a real code and a complex input sequence, it instead accepts only the real code. It then makes a copy of the code as gr_complex in order to perform correlation between the real and complex copies. This inefficient solution is a workaround for the fact that the current iteration of the volk-gnsssdr library contains functions for correlating complex valued inputs with real valued codes, but does not include the operators necessary to perform standard real-valued autocorrelations. This may be rectified in a future update.
An important feature of this measurement model implementation is that, as previously described, the measurement model needs to be able to perform arbitrary evaluations of the autocorrelation function of the local code. To this end, the functional which implements this needs to be extended to include an instance of Cpu_Autocorrelator_Real_Codes, which may be found in the cpu_autocorrelator_real_codes tracking library. This object adapts the Cpu_Multicorrelator_Real_Codes object. Instead of accepting a real code and a complex input sequence, it instead accepts only the real code. It then makes a copy of the code as gr_complex in order to perform correlation between the real and complex copies. This inefficient solution is a workaround for the fact that the current iteration of the volk-gnsssdr library contains functions for correlating complex valued inputs with real valued codes, but does not include the operators necessary to perform standard real-valued autocorrelations. This may be rectified in a future update.
Testing and Results
Testing of the joint_veml_tracking GNU radio block was performed by implementing an adapter block and unit test for running this tracking block with Galileo E1 signals. The tracking block and unit test can be found in the GNSS-SDR source repository here and here respectively. As before, the adapter and unit test are based on those implemented for Galileo E1 DLL+PLL tracking, however the joint code-carrier tracking implementation does not pass this test as running the tracking block results in a buffer error from the GNU radio kernel.

As of the writing of this report, this issue remains unresolved. It is hypothesized that this issue arises from an issue within the GNU radio architecture resulting from having too many instances of cpu_autocorrelator_real_codes being polled at a given time. Although it was not possible to investigate this further within the timeframe provided for Google Summer of code 2019, the proposed solution is to develop a more efficient way of evaluating the local code autocorrelation function, and this should be the subject of future work.
Conclusions and Future Work
Over the course of Google Summer of Code 2019 we have made several contributions to GNSS-SDR open-source GNSS receiver project. As the report shows, although each of the goals was met in part there is still significant work left to be done before these Gaussian filter based implementations are able to perform to the level of the standard locked loop implementations. Nevertheless, significant progress has been made with regard to building the software foundations for each of these these novel tracking architectures, and it is our firm belief that with a bit more work in tuning and bugfixing, these implementations may soon be made operational.
In summary, the contributions we have made this summer began with the development of a set of modular support libraries for building nonlinear models and applying them to the task of tracking with various Gaussian tracking implementations. Following this, we incorporated those nonlinear modelling and tracking libraries into the development of discriminator free, mixed tracking architecture based on cubature Kalman filter and DLL based carrier and code tracking respectiveily. Finally, we expanded the discriminator free mixed implementation to include a nonlinear code error estimation model, including the inclusion of code for performing autocorrelations with the local code.
The immediate future work is self evident: issues remain in getting the mixed tracking architecture to perform to the standard of the traditional DLL+PLL architecture, and in getting the joint tracking architecture to operate correctly within the GNU radio framework. Following this, there are many possible directions where this research can be taken but one in particular stands out as being of immediate interest. Although not included in this year's Google Summer of Code goals, one of the motivations for this year's contribution was to facilitate the use of the Bayesian Covariance estimation method that we worked on building in our 2018 Google Summer of Code contribution to the GNSS-SDR project. Finally, additional nonlinear tracking methodologies, including those based on Monte Carlo methods rather than Kalman architectures, could be built and tested based on the framework that we constructed in this contribution.
